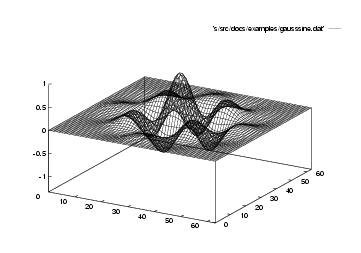
There is good help within gnuplot, available by typing help.
3.2.2 IDL
IDL is much more powerful and flexible than gnuplot, and has a correspondingly longer learning curve. It’s never been accused of being elegant, but with only a bit of headbanging, I’ve always managed to get it to do what I wanted (I’ve always seen it as reminiscent of Fortran in this respect).
Several missions have used IDL as the language in which they have written their data-analysis software, and Starlink is currently experimenting with providing IDL interfaces to important Starlink applications, which is possible because IDL can link to codes written in languages such as Fortran or C. IDL is moving towards being a core facility at Starlink sites.
IDL displays data in arrays as part of a generic set of array manipulations. For example, the data in the file
gausssine.dat was produced by the following sequence of IDL commands:
d=fltarr(64,64)
for i=0,63 do d(i,*)=sqrt(x+(i-32)^2)
a3=exp(-(d/15)^2)
s=sin(findgen(64)/63*5*3.141592657)
s2=s#s
m=s2*a3
The function findgen(N) returns a float array (indexed from 0 to
)
in which the value of each element is the same as its index; performing an arithmetic operation
such as subtraction or exponentiation on an array performs it on each element of the array;
fltarr declares an array of floats of the specified dimensions; the array reference d(i,*) refers
to the entire i’th row of d; the operator # forms the direct product of the two vectors. The result
of this is to set d to be an array where each element is the euclidean distance from element
(32,32)1.
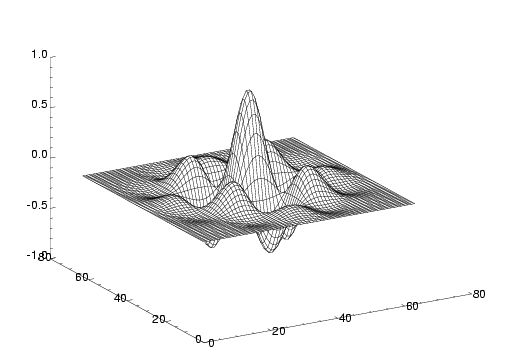
Once we have the data in the array m, we can produce a surface plot with surface,m, and then go on to annotate
it, rotate it, shade it, contour it, with the large collection of options and parameters to the surface command. We
can produce PostScript output with the following sequence of commands:
set_plot, ’ps’ ; use the postscript output driver
device, /encap, filename=’gausssine-idl.eps’
; produce encapsulated postscript
surface, m
device, /close ; close the file
This produces the EPS file shown in 3.2. A minor, but persistent, irritation with IDL is that, although its input and output facilities are as flexible as, say, Fortran’s (which they closely resemble), it doesn’t come with a function for dealing with the common case of data printed out in columns (the only case gnuplot naturally deals with). Fortunately, such a function is not only easy to write, but a useful example, too. See A.8.
IDL comes with rather good manuals, the reference parts of which are available on-line by typing ? at the IDL
prompt.
See appendix B of SUN/55 for a description of how to import data in the Starlink NDF format into IDL.
3.2.3 DX
IBM’s Data Explorer is also available on some Starlink machines. I don’t have personal experience of it, but there is a Starlink manual for it in SUN/203, “SX and DX — IBM data explorer for data visualisation” and a Starlink DX cookbook in SC/2.
In his overview of visualisation systems in SG/8, Clive Davenhall says of DX:
IBM Data Explorer (DX) is a general-purpose software package for data visualisation and analysis. It employs a data-flow driven client-server execution model and provides a comprehensive range of data manipulation, visualisation and display functions. Visualisations can be generated using a visual programming editor or a text-based scripting language. DX is the visualisation package recommended by Starlink, particularly for three-dimensional scalar and vector data. Starlink has produced a set of enhancements to DX. If you are using DX at a Starlink site then these enhancements should be available automatically. The use of DX at Starlink sites and the Starlink enhancements to DX are documented in SUN/203.
3.2.4 PGPLOT
The above recommendations describe standalone packages which work on data produced by your code in a separate step. An alternative route is to incorporate the plotting facilities within your program, and the recommended way of doing this is by using the PGPLOT library.
The library, which was written to support astronomical applications, consists of a collection of high-level routines for producing plots, maps and images either on-screen or as Postscript to a file. Refer to SUN/15, “PGPLOT — Graphics Subroutine Library” for further details, or to the PGPLOT home page at .
Note that there are two versions of PGPLOT currently available on Starlink, ‘native’ PGPLOT, and a Starlink version which uses GKS. The latter is being deprecated, with a view to being ultimately phased out, and this will affect how you link your program against the library. At the time of writing (December 1998), the way in which the dual versions will be supported has not been finalised; ask your system manager for advice.
3.3 Producing images
If you wish to include images in your LaTeX output, do so using the standard graphics package. That
is, include in your file the command \usepackage{graphics} (if you’re obliged to use the old
LaTeX2.09, you can use the epsf option to the document style). Include the graphics with the command
\starincludegraphics{file.eps}. So how do you produce the postscript?
An important point is that the postscript should be encapsulated postscript. This is postscript intended to be
incorporated within another document: it has a BoundingBox comment at the top of the file, and typically has
the extension .eps.
See 3.2 for details of how to produce EPS plots from gnuplot and IDL.
If it’s diagrams you want to produce, then xfig has its adherents. There’s a large manual page for xfig, but you
can do pretty well just starting it up, and pointing and clicking.
If point and click isn’t your style, try MetaPost. This is a variant of Knuth’s MetaFont (which is used for
designing TeX fonts), which produces postscript instead. To produce a document using MetaPost, you produce
a text file specifying the objects you want to draw and their spatial relationships. It can be hard work, but the
results can look very good. If you wished to automate producing diagrams, perhaps because you
want to produce a set of diagrams which are systematically different, then MetaPost could very
well help you with this. See .../texmf/doc/metapost under the (Starlink) TeX tree for further
details.
1IDL experts will know that the common IDL idiom for this is d=shift(dist(64),32,32), but have you ever actually compared dist
with its documentation? The documentation for dist suggests that this idiom wouldn’t work, but the function’s actual behaviour seems to
(substantially) depart from the claimed behaviour in exactly the right way.