
An effect which must be corrected when calibrating instrumental magnitudes is the atmospheric extinction or the dimming of starlight by the terrestrial atmosphere. The longer the path length the starlight traverses through the atmosphere the more it is dimmed. Thus, a star close to the horizon will be dimmed more than one close to the zenith, and the observed brightness of a given star will change throughout a night, as its zenith distance varies.
The path length through the atmosphere is known as the air mass. Consider an observation through the blanket of the atmosphere around the curved surface of the Earth. At any particular wavelength, , we can relate , the magnitude of the observed object outside the atmosphere, to , the magnitude of the observed object at the surface of the earth, by:
| (11) |
where is the air mass, is the extinction coefficient at wavelength and is the zenith distance (the angular distance of the object from the zenith at the time of observation). is defined as the number of times the quantity of air seen along the line of sight is greater than the quantity of air in the direction of the zenith and will vary as the observed line of sight moves away from the zenith, that is, as increases. Note that the air mass is a normalised quantity and the air mass at the zenith is one.
For small zenith angles is a reasonable approximation, but as increases, refraction effects, curvature of the atmosphere and variations of air density with height can become important. Hardie[35] gives a more refined relationship:
| (12) |
and Young and Irvine[80] propose:
| (13) |
Both these equations imply the use of , the true zenith angle, that is, the zenith angle to the observed object in the absence of the atmosphere as opposed to the apparent zenith angle affected by refraction effects.
For purposes of illustration the approximate air mass is tabulated as a function of zenith distance in Table 3. Note that the air mass remains quite small for , reaches 2.0 at and increases rapidly thereafter.
| 1.00 | 1.31 | ||
| 5 | 1.00 | 45 | 1.41 |
| 10 | 1.02 | 50 | 1.56 |
| 15 | 1.04 | 55 | 1.74 |
| 20 | 1.06 | 60 | 2.00 |
| 25 | 1.10 | 65 | 2.37 |
| 30 | 1.16 | 70 | 2.92 |
| 35 | 1.22 | ||
The atmospheric extinction coefficient, , can be determined by observing the same object (through an appropriate filter) at several times during the night at varying zenith angles. When the observed magnitudes of the object are plotted against computed air mass (see Figure 4), they should lie on a straight line with a slope equal to . It is important to note that the extinction is dependent upon wavelength, being greater for blue light than red.

Traditionally the infrared region of the spectrum was considered to be wavelengths just longer than the reddest colours visible to the human eye, typically about 7000Å or (0.7m). However, in modern astronomical usage wavelengths up to about 10,000Å (or 1m) tend to be described as ‘optical’ and longer wavelengths as ‘infrared’. This terminology reflects both a change in the type of detector used and the behaviour of the terrestrial atmosphere at about 10,000Å. It is cumbersome to quote infrared wavelengths in Ångström and they are usually given in micron. The infrared region stretches to about 350m; longer wavelengths are referred to as the sub-millimetre part of the spectrum.
The terrestrial atmosphere is largely opaque at most infrared wavelengths longer than 1m, largely due to absorption by water vapour and carbon dioxide. However, there are a series of wavelength ranges or windows where the atmosphere is mostly transparent (see Figure 5). Ground-based infrared observations must be made in these windows. Each window corresponds to a band in the system (see Section 7) and the corresponding band and window have the same name.
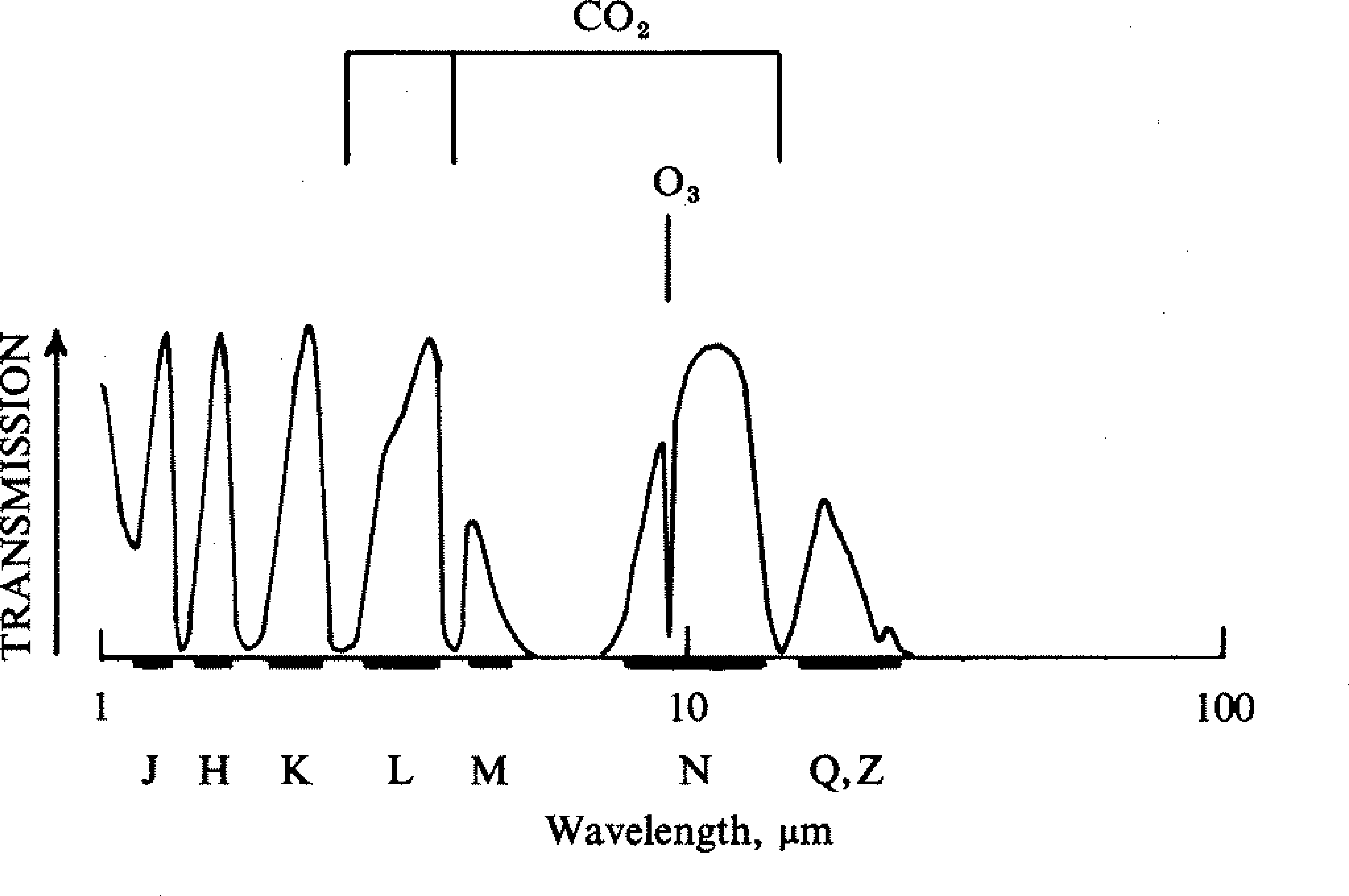
The width, maximum transmission and, to an extent, central wavelength of the windows vary with geographical location and in particular with altitude. They also vary with the current meteorological conditions. The windows are particularly sensitive to the amount of water vapour, which is why infrared observatories tend to be at high, dry sites. The variation in the infrared windows at different locations is the underlying reason for different versions of the system being used at different observatories, as mentioned in Section 7.